K Closest Points to Origin

Problem Overview

Difficulty: Medium

Given an array of points where points[i] = [xi, yi] and an integer k, return the k closest points to the origin (0, 0).

Note: Euclidean Distance To Origin = √(x² + y²)

Input: 
· points = [[1,3],[-2,2]]
· k = 1

Output: 
· [[-2,2]]

Explanation:
· [1,3] dist to origin = √10
· [-2,2] dist to origin = √8
· Since √8 < √10, return [-2,2]

---

Step 1: Clarify Requirements

• Are input points sorted?

  • No.

• Can k be 0 or more than total points?

  • No.

• Can multiple points have the same distance?

  • No.

• Can we return the output in any order?

  • Yes.

---

Step 2: Discuss Approaches

Approach 1: Sort All Points (Brute Force)

• Logic:

  • For each point:

    • Compute its distance to origin

  • Sort all these points by distance

  • Return first k points

• Big O:

  • Time Complexity: O(n·logn)

  • Space Complexity: O(n)

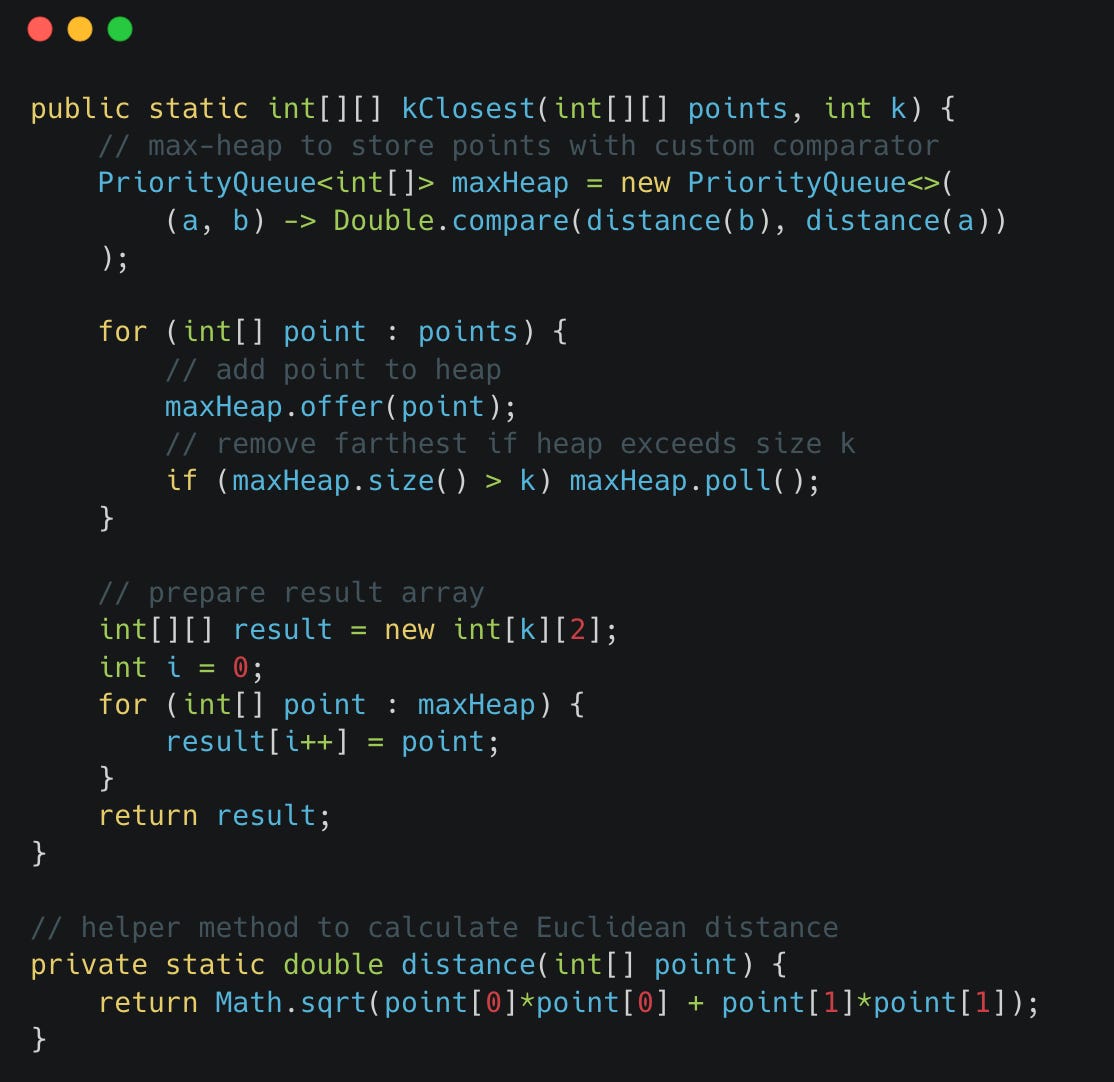
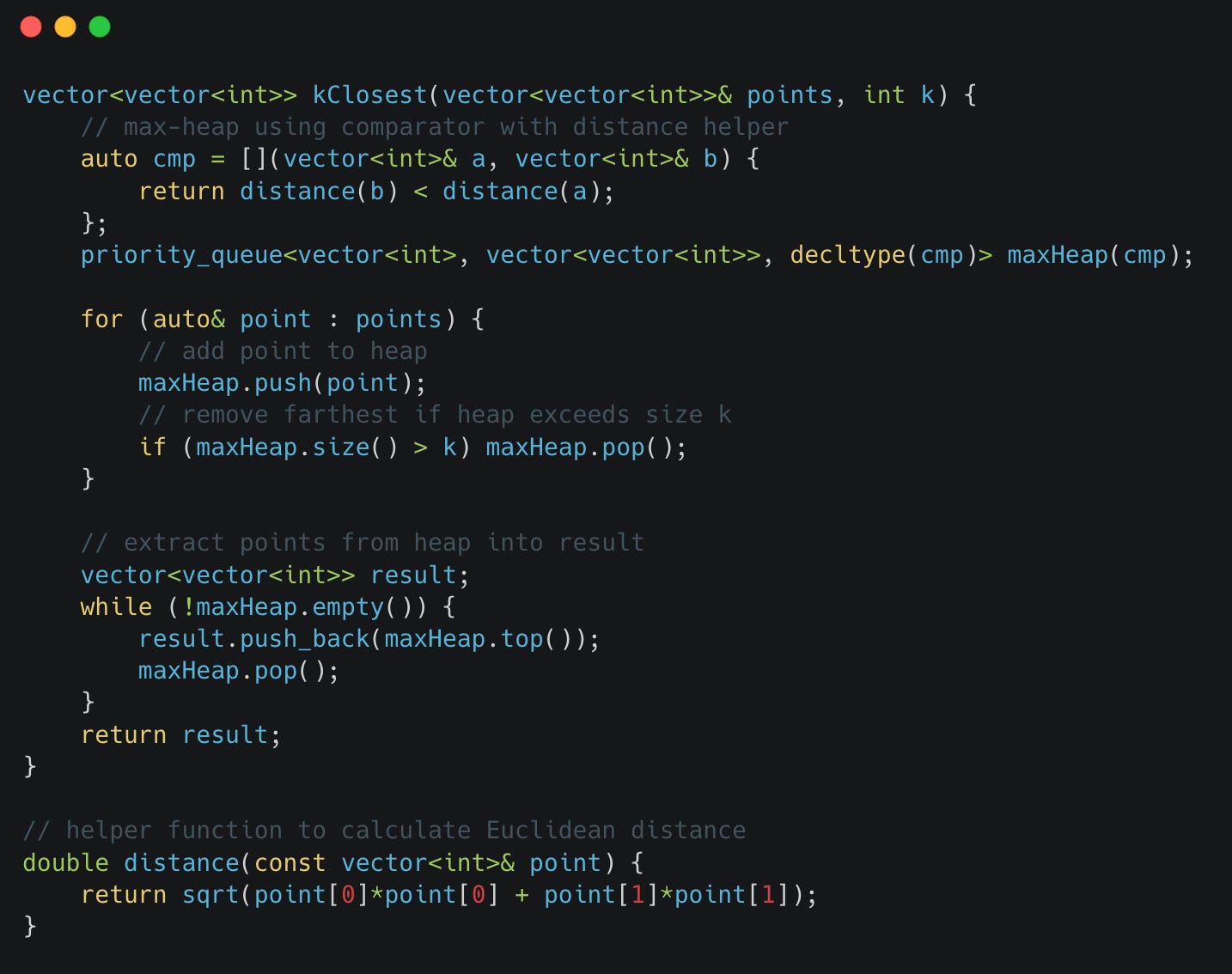
Approach 2: Use a Max-Heap (Optimal)

• Logic:

  • Use a max-heap of size k

  • For each point:

    • Compute its distance to origin

    • Push to heap

    • If heap size > k, remove the top

  • At the end:

    • Heap contains k-closest points

• Big O:

  • Time Complexity: O(n·logk)

  • Space Complexity: O(k)

---

Step 3: Write Code (Optimal)

Python

---

Java

---

C++

---

Step 4: Answer Follow-Ups

• Why use max-heap and not min-heap?

  • To keep the closest k points.

  • Easy to remove top (farthest point).

• What if two points are equidistant?

  • We can return either point.

  • Any valid answer is accepted.

• What if we wanted k farthest points?

  • Use a min-heap of size k.

  • Push (dist, [x,y]) into heap.

  • If heap size > k, remove the top.

  • At the end, heap contains the result.

---

👨‍💻 Need Interview Practice?

• Book a 1:1 with me

• Book Here: Booking URL